ТЕКСТ ДЛЯ ЧТЕНИЯ
1. Понятие обыкновенной дроби ![]()
Возьмём 1 (единицу) и разделим её на три равные части (рисунок 4.1). Одна третья часть единицы – это дробь ![]() (одна третья). Две третьих части единицы – это дробь
(одна третья). Две третьих части единицы – это дробь ![]() (две третьих). Три третьих части единицы – это дробь
(две третьих). Три третьих части единицы – это дробь ![]() (три третьих).
(три третьих). 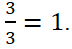
![]()
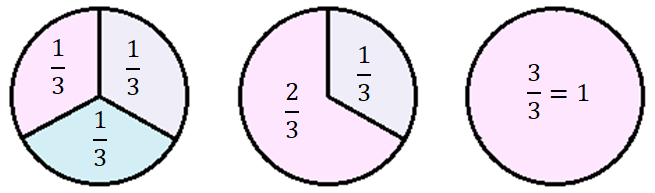
Рисунок 4.1
Числа 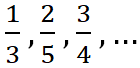 – это обыкновенные дроби.
– это обыкновенные дроби. ![]()
Запись вида ![]() – это обыкновенная дробь.
– это обыкновенная дробь. ![]()
Число p – это числитель дроби. Число p стоит над чертой. ![]()
Число q – это знаменатель дроби. Число q стоит под чертой. ![]()
Черта дроби – это знак деления числителя на знаменатель. ![]()
Знаменатель дроби показывает, на сколько частей мы разделили число один (единицу). Числитель дроби показывает, сколько частей мы взяли. Поэтому, чтобы получить число ![]() из числа один, надо разделить число один на q равных частей и взять p таких частей.
из числа один, надо разделить число один на q равных частей и взять p таких частей. ![]()
Любое число – это дробь, у которой знаменатель равен числу один: 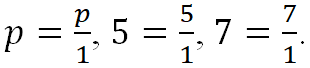
![]()
Запомните, как читать порядковые числительные!
|
Какой? |
Какая? |
Какое? |
Какие? |
Каких? |
|
|
1 |
Первый |
Первая |
Первое |
Первые |
Первых |
|
2 |
Второй |
Вторая |
Второе |
Вторые |
Вторых |
|
3 |
Третий |
Третья |
Третье |
Третьи |
Третьих |
|
4 |
Четвёртый |
Четвёртая |
Четвёртое |
Четвёртые |
Четвёртых |
|
5 |
Пятый |
Пятая |
Пятое |
Пятые |
Пятых |
|
6 |
Шестой |
Шестая |
Шестое |
Шестые |
Шестых |
|
7 |
Седьмой |
Седьмая |
Седьмое |
Седьмые |
Седьмых |
|
10 |
Десятый |
Десятая |
Десятое |
Десятые |
Десятых |
|
20 |
Двадцатый |
Двадцатая |
Двадцатое |
Двадцатые |
Двадцатых |
|
21 |
Двадцать первый |
Двадцать первая |
Двадцать первое |
Двадцать первые |
Двадцать первых |
|
30 |
Тридцатый |
Тридцатая |
Тридцатое |
Тридцатые |
Тридцатых |
|
40 |
Сороковой |
Сороковая |
Сороковое |
Сороковые |
Сороковых |
|
50 |
Пятидесятый |
Пятидесятая |
Пятидесятое |
Пятидесятые |
Пятидесятых |
|
52 |
Пятьдесят второй |
Пятьдесят вторая |
Пятьдесят второе |
Пятьдесят вторые |
Пятьдесят вторых |
|
100 |
Сотый |
Сотая |
Сотое |
Сотые |
Сотых |
|
200 |
Двухсотый |
Двухсотая |
Двухсотое |
Двухсотые |
Двухсотых |
|
1000 |
Тысячный |
Тысячная |
Тысячное |
Тысячные |
Тысячных |
Запомните!

Запомните, как читать обыкновенные дроби! ![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
двести вторая |
|
|
|
|
|
|
|
|
|
|
|
2. Правильные, неправильные и смешанные дроби ![]()
Правильная дробь– это дробь, у которой числитель меньше, чем знаменатель. Число ![]() – это правильная дробь, так как числитель 2 меньше, чем знаменатель 5.
– это правильная дробь, так как числитель 2 меньше, чем знаменатель 5. ![]()
Неправильная дробь – это дробь, у которой числитель больше или равен знаменателю. Число ![]() – это неправильная дробь, так как числитель 5 больше, чем знаменатель 2. Число
– это неправильная дробь, так как числитель 5 больше, чем знаменатель 2. Число ![]() – это тоже неправильная дробь, так как числитель 2 равен знаменателю 2.
– это тоже неправильная дробь, так как числитель 2 равен знаменателю 2. ![]()
Пример. 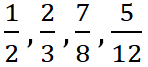 – это правильные дроби.
– это правильные дроби. ![]()
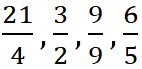 – это неправильные дроби.
– это неправильные дроби. ![]()
Запомните, как читать целые части! ![]()
|
1 – одна целая |
2 – две |
|
21 – двадцать
31 – тридцать одна целая |
22 |
Запомните, как читать смешанные дроби! ![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Неправильную дробь ![]() можно записать так:
можно записать так: ![]()
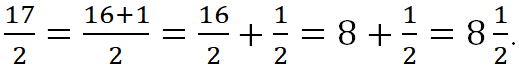
![]()
![]() – это смешанная дробь. Смешанная дробь имеет две части: 8 – это целая часть,
– это смешанная дробь. Смешанная дробь имеет две части: 8 – это целая часть, ![]() – это дробная часть.
– это дробная часть. ![]()
Неправильные дроби можно записать как смешанные: ![]()
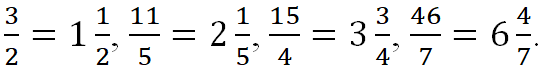
![]()
Смешанную дробь ![]() можно записать так:
можно записать так: ![]()
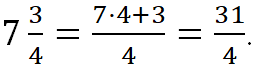
![]()
Смешанные дроби можно записать как неправильные: ![]()
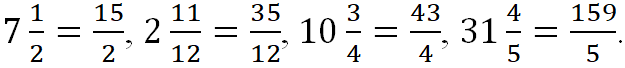
![]()
3. Основное свойство дроби ![]()
Если числитель и знаменатель дроби умножить на одно и то же число, то получится дробь, которая равна данной дроби: 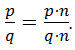
![]()
С помощью основного свойства для любой дроби можно записать сколько угодно дробей, которые ей равны. Например, 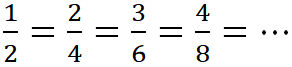 или
или 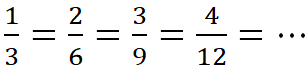 . Дроби
. Дроби ![]() определяют одно и то же число, которое записано в разных формах.
определяют одно и то же число, которое записано в разных формах. ![]()
Основное свойство дроби можно записать в обратном порядке: ![]()
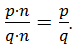
![]()
4. Сокращение дробей ![]()
Основное свойство дроби можно использовать, чтобы сократить дробь. ![]()
Сократить дробь – это значит числитель и знаменатель дроби разделить на общий множитель, который не равен единице. При этом получится дробь, которая равна данной дроби. ![]()
Если дробь ![]() можно сократить, то это сократимая дробь.
можно сократить, то это сократимая дробь. ![]()
Если числитель и знаменатель дроби ![]() не имеют общих простых делителей, то дробь
не имеют общих простых делителей, то дробь ![]() – это несократимая дробь.
– это несократимая дробь. ![]()
Рассмотрим дробь ![]() . Её можно сократить на 5.
. Её можно сократить на 5. ![]()
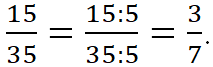
![]()
![]() – это сократимая дробь,
– это сократимая дробь, ![]() – это несократимая дробь.
– это несократимая дробь. ![]()
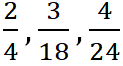 – это сократимые дроби,
– это сократимые дроби, 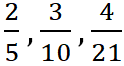 – это несократимые дроби.
– это несократимые дроби. ![]()
5. Приведение дробей к наименьшему общему знаменателю ![]()
Дроби 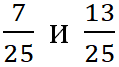 имеют одинаковые знаменатели, то есть они имеют общий знаменатель. Дроби
имеют одинаковые знаменатели, то есть они имеют общий знаменатель. Дроби 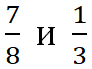 имеют разные знаменатели. Но их можно привести к общему знаменателю с помощью основного свойства дроби. Для этого надо найти число, которое делится на 8 и на 3. Например, 24. Приведём дроби к общему знаменателю 24. Для этого надо умножить числитель и знаменатель дроби
имеют разные знаменатели. Но их можно привести к общему знаменателю с помощью основного свойства дроби. Для этого надо найти число, которое делится на 8 и на 3. Например, 24. Приведём дроби к общему знаменателю 24. Для этого надо умножить числитель и знаменатель дроби ![]() на дополнительный множитель 3 (24 : 8 = 3). Дополнительный множитель для дроби
на дополнительный множитель 3 (24 : 8 = 3). Дополнительный множитель для дроби ![]() равен 8 (24 : 3 = 8). Получим:
равен 8 (24 : 3 = 8). Получим: ![]()
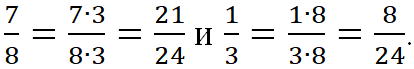
![]()
Чаще всего дроби приводят к наименьшему общему знаменателю (НОЗ). Наименьший общий знаменатель равен наименьшему общему кратному (НОК) знаменателей данных дробей. ![]()
Пример. Приведём дроби 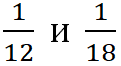 к наименьшему общему знаменателю.
к наименьшему общему знаменателю. ![]()
Найдём НОЗ(12; 18) = НОК(12; 18). 12 = 2 · 2 · 3, 18 = 2 · 3 · 3 ⇒ НОЗ(12; 18) = 2 · 2 · 3 · 3 = 36. Дополнительный множитель дроби ![]() – это 3, так как 36 : 12 = 3. Дополнительный множитель дроби
– это 3, так как 36 : 12 = 3. Дополнительный множитель дроби ![]() – это 2, так как 36 : 18 = 2. Следовательно,
– это 2, так как 36 : 18 = 2. Следовательно, 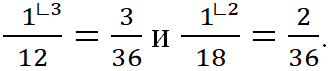
![]()
6. Сравнение дробей ![]()
1. Если знаменатели дробей одинаковые, то больше та дробь, у которой числитель больше. ![]()
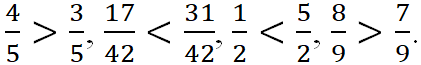
![]()
2. Если числители дробей одинаковые, то больше та дробь, у которой знаменатель меньше. ![]()
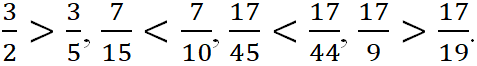
![]()
3. Если у дробей числители и знаменатели разные, то сначала дроби надо привести к наименьшему общему знаменателю, а потом сравнить. ![]()
Пример. Сравним дроби 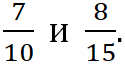
![]()
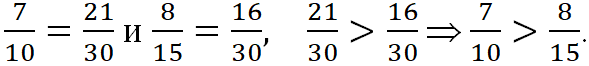
![]()
Правильная дробь меньше 1 (единицы), а неправильная дробь больше или равна 1 (единице). ![]()
7. Сложение и вычитание обыкновенных дробей ![]()
Чтобы сложить (вычесть) дроби с общим знаменателем, надо сложить (вычесть) их числители, а знаменатель оставить без изменений. ![]()
Например, 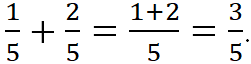
![]()
Чтобы сложить (вычесть) дроби с разными знаменателями, надо сначала привести дроби к общему знаменателю, а затем сложить (вычесть) их числители и записать общий знаменатель. ![]()
Например, 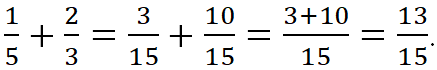
![]()
Чтобы сложить (вычесть) смешанные дроби, надо сложить (вычесть) целые части, затем сложить (вычесть) дробные части и полученные результаты сложить. ![]()
Например, 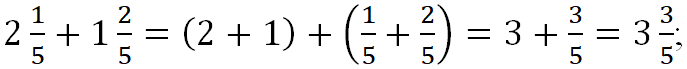
![]()
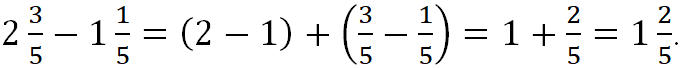
![]()
8. Умножение и деление обыкновенных дробей ![]()
Чтобы умножить число на дробь, надо числитель дроби умножить на это число, а знаменатель оставить без изменения. ![]()
Пример. 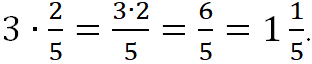
![]()
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей: 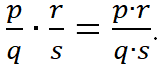
![]()
Пример. 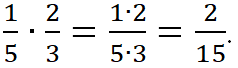
![]()
Дробь ![]() – это число, обратное для дроби
– это число, обратное для дроби ![]() . Числа
. Числа ![]() и
и ![]() – это взаимно обратные числа. Взаимно обратные числа – это числа, произведение которых равно единице.
– это взаимно обратные числа. Взаимно обратные числа – это числа, произведение которых равно единице. ![]()
Пример. ![]() и
и ![]() – это взаимно обратные числа, так как
– это взаимно обратные числа, так как 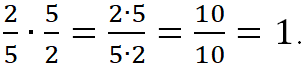
![]()
Чтобы разделить дробь на дробь, надо делимое умножить на дробь, обратную делителю. ![]()
Пример. 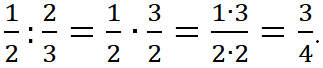
![]()
При умножении и делении смешанных дробей удобно сначала записать их в виде неправильных дробей. ![]()
Пример. 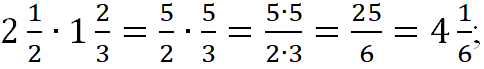
![]()
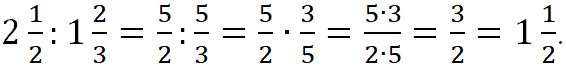
![]()
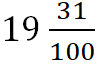 – девятнадцать целых,
– девятнадцать целых,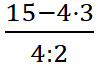 – дробь, в числителе 15 – 4 · 3
– дробь, в числителе 15 – 4 · 3