ТЕКСТ ДЛЯ ЧТЕНИЯ
1. Выражения с переменными 
Запись, которая состоит только из чисел, знаков действий и скобок, – это числовое выражение.
Выражение, которое состоит из чисел, знаков действий сложения, вычитания, умножения, деления, возведения в целую степень и извлечения корня, скобок и букв – это выражение с переменными.
Например, 9x + 17, 2x – 3y2, 5x2 + 2x + 3,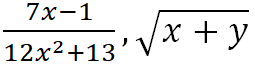 
– это выражения с переменными.
Буквы в математике обозначают числа. Вместо букв в выражение можно подставить разные числа. При этом значения букв будут меняться. Поэтому буквы в математике – это переменные.
Например, в выражении x + 7 одна переменная – это x, а в выражении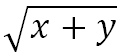 
две переменные – это x и y.
Чтобы найти значение выражения с переменными, необходимо:
1) значения всех переменных подставить в выражение;
2) выполнить все действия.
Например, чтобы найти значение выражения 9x + 17, если x = 1, нужно вместо переменной x подставить её значение: 9x + 17 = 9 · 1 + 17 = 26.
Значение выражения с переменной зависит от значения этой переменной, то есть при разных значениях переменной выражение с переменной может принимать разные значения.
Например, если x = 1, то 9x + 17 = 9 · 1 + 17 = 26;
если x = 4, то 9x + 17 = 9 · 4 + 17 = 53 и так далее.
2. Функция
Переменная y называется функцией переменной x, если каждому допустимому значению x соответствует единственное значение y. При этом используют запись y = f(x) и говорят «игрек равен эф от икс».
Переменную x называют независимой переменной (аргументом), а переменную y – зависимой переменной. Значение y, которое соответствует заданному значению x, называют значением функции.
При некоторых значениях переменных выражение с переменной может не иметь смысла.
Например, если x = 5, то выражение 
не имеет смысла, потому что знаменатель x – 5 = 5 – 5 = 0, а на нуль делить нельзя.
Числовые значения переменных, при которых выражение имеет смысл (имеет числовое значение) – это допустимые значения переменных.
Множество всех допустимых значений переменных выражения – это область допустимых значений (ОДЗ) выражения.
Пример. Для выражения ОДЗ имеет вид: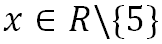 
(все действительные числа, кроме числа 5) или 
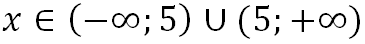(объединение промежутков от минус бесконечности до числа 5 и от числа 5 до плюс бесконечности).
Областью определения D(f ) (дэ от эф) функции y = f (x) называется множество всех действительных значений аргумента x, при которых функция может иметь действительное значение.
Пример. Областью определения функции y = x является множество всех действительных чисел R: D(f ) = R, а для функции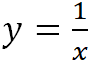 
областью определения является множество R, кроме x = 0: D(f ) = R \ {0}.