Для любой дроби можно записать сколько угодно дробей, которые ей равны. ![]()
Например, 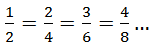 или
или 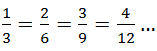
![]()
Дроби 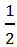 и
и 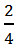 определяют одно и то же число, которое записано в разных формах.
определяют одно и то же число, которое записано в разных формах. ![]()
Запомните основное свойство дроби! ![]()
|
Если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится дробь, которая равна данной дроби: 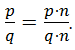
|
Основное свойство дроби можно записать в обратном порядке:
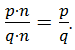
![]()
Если n > 1 (числа один), то дробь можно сократить. ![]()
Если числитель и знаменатель дроби имеют общий множитель, который не равен 1, то дробь можно сократить на этот множитель. При этом получится дробь, которая равна данной дроби. ![]()
![]()
Если числитель и знаменатель дроби 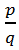 не имеют общих простых делителей, то дробь
не имеют общих простых делителей, то дробь 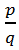 – это несократимая дробь.
– это несократимая дробь. ![]()
Дроби 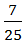 и
и 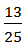 имеют одинаковые знаменатели, то есть они имеют общий знаменатель. Дроби
имеют одинаковые знаменатели, то есть они имеют общий знаменатель. Дроби 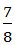 и
и 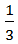 имеют разные знаменатели. Но их можно привести к общему знаменателю с помощью основного свойства дроби. Для этого надо найти число, которое делится на 8 и на 3. Например, 24. Приведём дроби к общему знаменателю 24. Для этого надо умножить числитель и знаменатель дроби
имеют разные знаменатели. Но их можно привести к общему знаменателю с помощью основного свойства дроби. Для этого надо найти число, которое делится на 8 и на 3. Например, 24. Приведём дроби к общему знаменателю 24. Для этого надо умножить числитель и знаменатель дроби 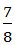 на дополнительный множитель 3 (24 : 8 = 3). Дополнительный множитель для дроби
на дополнительный множитель 3 (24 : 8 = 3). Дополнительный множитель для дроби 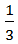 равен 8 (24 : 3 = 8). Получим:
равен 8 (24 : 3 = 8). Получим:
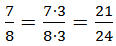 и
и 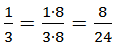 .
. ![]()
Чаще всего дроби приводят к наименьшему общему знаменателю. Наименьший общий знаменатель равен наименьшему общему кратному знаменателей данных дробей. ![]()
![]()
Дроби, как и натуральные числа, можно сравнивать. ![]()
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше. ![]()
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше. ![]()
Чтобы сравнить две дроби, надо привести их к общему знаменателю, а затем сравнить числители. ![]()
Правильная дробь меньше единицы, а неправильная дробь больше или равна единице. ![]()
Рассмотрим, как выполнить арифметические операции с дробями. ![]()
Чтобы сложить (вычесть) дроби с общим знаменателем, надо сложить (вычесть) их числители, а знаменатель оставить без изменений. ![]()
Например, 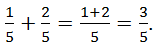
![]()
Чтобы сложить (вычесть) дроби с разными знаменателями, надо сначала привести дроби к общему знаменателю, а затем сложить (вычесть) их числители, и записать общий знаменатель. ![]()
Например, 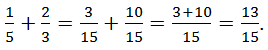
![]()
Сложение и вычитание смешанных дробей можно выполнять с помощью законов сложения. Чтобы сложить (вычесть) смешанные дроби, надо сложить (вычесть) целые части, затем сложить (вычесть) дробные части и полученные результаты сложить. ![]()
Например, 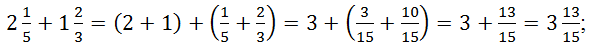
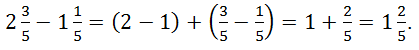
![]()
Чтобы сложить (вычесть) смешанные дроби, можно сначала записать дроби как неправильные, затем привести дроби к общему знаменателю, сложить числители и записать общий знаменатель. ![]()
Например, 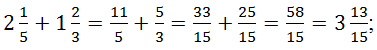
![]()
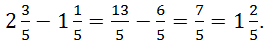
![]()
![]()
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей: ![]()
![]()
Например, 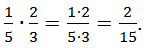
![]()
Чтобы умножить натуральное число на дробь, надо числитель дроби умножить на это натуральное число, а знаменатель оставить без изменения. ![]()
Например, 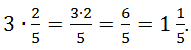
![]()
Дробь 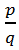 – это число, обратное для дроби
– это число, обратное для дроби 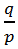 («ку пэтых»). Числа
(«ку пэтых»). Числа 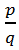 и
и 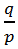 – это взаимно обратные числа (здесь p и q – натуральные числа). Произведение взаимно обратных чисел равно 1.
– это взаимно обратные числа (здесь p и q – натуральные числа). Произведение взаимно обратных чисел равно 1. ![]()
Например, 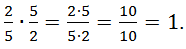
![]()
Частное двух дробей равно дроби, которая при умножении на делитель даёт делимое. ![]()
Чтобы разделить дробь на дробь, надо делимое умножить на дробь, обратную делителю. ![]()
Например, 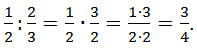
![]()
При умножении и делении смешанных дробей удобно сначала записать их в виде неправильных дробей. ![]()
Например, 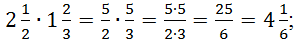
![]()
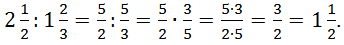
![]()
![]()
Все законы сложения (коммутативный и ассоциативный) и умножения (коммутативный, ассоциативный, дистрибутивный) выполняются и для дробей. ![]()