Частное двух чисел a и b, которые не равны нулю, – это отношение a к b. Числа a и b – это члены отношения. Например, 8 : 2 или 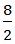 – это отношение числа 8 к числу 2 (отношение восьми к двум). 

Равенство двух отношений – это пропорция. Пропорцию a : b = c : d или 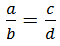 читаем так: «отношение a к b равно отношению c к d» или «a относится к b как c относится к d». 

Числа a и d – это крайние члены пропорции. Числа b и c – это средние члены пропорции. 

Из пропорции 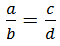 следует пропорция 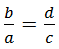, потому что если дроби равны, то и обратные им дроби равны. 

Основное свойство пропорции. 

Произведение крайних членов пропорции равно произведению средних членов пропорции: если 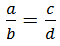  , то a · d = b · c.  

Если один из членов пропорции неизвестен и необходимо его определить, то говорят, что нужно решить пропорцию. 

Чтобы найти неизвестный крайний член пропорции, надо произведение средних членов пропорции разделить на известный крайний член пропорции. 

Чтобы найти неизвестный средний член пропорции, надо произведение крайних членов пропорции разделить на известный средний член пропорции. 

В математике (и в других науках) используется понятие «величина». Величина – это результат измерения. Величина определяется числом и единицей измерения. Например, длина стола равна одному метру (1 м). 

Отношение величин с одинаковыми единицами измерения – это число. Например, .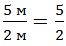 

Отношение величин с разными единицами измерения определяет новую величину. Например, .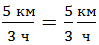 

Величины x и y называются прямо пропорциональными, если при увеличении величины x в несколько раз величина y увеличивается во столько же раз. 

Величины x и y называются обратно пропорциональными, если при увеличении величины x в несколько раз величина y уменьшается во столько же раз. 

В десятичной системе часто используются сотые части. 

Сотая часть числа – это процент. Обозначается процент знаком %. 

Рассмотрим три основных типа задач на проценты:

1) найти процент от данного числа;

2) найти число по его процентам;

3) найти процентное отношение чисел. 

Чтобы решить задачи 1 и 2, надо знать, что процент – это одна сотая часть числа и составить пропорцию. Решение задачи третьего типа связано с выражением в процентах отношения двух чисел. Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100. 

Запомните, как читать проценты!