Положительные дробные числа – это положительные обыкновенные дроби. Если перед положительной дробью поставить знак плюс (+), то дробь не изменится:

 

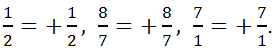
Если перед положительной дробью поставить знак минус (–), то получится новое число – отрицательное дробное число или отрицательная дробь. Например, числа 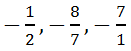– это отрицательные дроби. 

Число, которое можно записать в виде 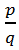, где p, q – целые числа и q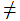0, – это рациональное число или дробь. Например, числа  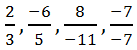 – это рациональные числа. 

Дроби, которые отличаются только знаком, – это противоположные дроби. У противоположных дробей модули одинаковые. Все свойства модуля выполняются и для рациональных чисел. 

Основное свойство дроби верно не только для положительных дробей, но и для всех рациональных чисел. С помощью основного свойства дроби можно привести дроби к новому знаменателю и сократить дробь. 

Рациональное число – это:

а) положительная дробь, если p, q имеют одинаковый знак;

б) отрицательная дробь, если p, q имеют разные знаки;

в) число 0, если p = 0. 

Для любого целого числа p верно равенство: 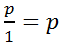. Оно означает, что любое целое число является рациональным числом. 

Чтобы сравнить две любые дроби, сначала надо привести их к общему положительному знаменателю. 

Из двух дробей с общим положительным знаменателем больше та, у которой числитель больше. 

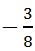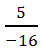Например, сравним дроби  и  . Приведём дроби к общему положительному знаменателю: 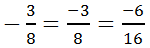; 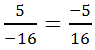. Так как –6 < –5, то  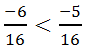и .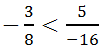  

Из общего правила сравнения целых чисел следует, что положительная дробь больше отрицательной дроби и больше нуля, отрицательная дробь меньше нуля. 

Все арифметические действия с рациональными числами выполняются также как и с положительными дробями. Для рациональных чисел выполняются все законы сложения и умножения.