Сложение и вычитание десятичных дробей выполняются так же, как сложение и вычитание обыкновенных дробей. Сначала надо привести дроби к общему знаменателю, а затем выполнить действие. 

Привести десятичные дроби к общему знаменателю – значит уравнять число знаков после запятой (в дробной части). 

Например, выполним действия 0,2 + 0,05 – 0,023:

0,2 + 0,05 – 0,023 = 0,200 + 0,050 – 0,023 = 0,227. 

Чтобы перемножить две десятичные дроби, надо:

1) убрать запятую;

2) перемножить новые числа;

3) в полученном произведении справа отделить запятой столько цифр, сколько их было после запятых во всех множителях вместе. 

Например,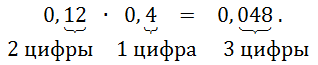   

Чтобы разделить десятичную дробь на целое число, надо сначала разделить нацело целую часть на это число, поставить запятую, а затем разделить дробную часть на это число. 

Чтобы разделить десятичную дробь на десятичную дробь, надо сначала перенести запятую у делимого и делителя вправо на столько цифр, сколько их у делителя в дробной части. Затем выполнить деление на целое число. 

Десятичные дроби бывают конечные и бесконечные. В конечной десятичной дроби после запятой стоит конечное число цифр. В бесконечной десятичной дроби после запятой стоит бесконечно много цифр. 

Например, 1,1; 7,03; 0,004 – это конечные дроби;

                   0,171717…; 0,10110111011110… – это бесконечные дроби. 

Если конечную десятичную дробь записать в виде обыкновенной несократимой дроби 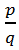, то её знаменатель q не имеет других простых делителей, кроме 2 и 5. 

Например, .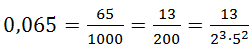 

Верно и обратное. Если знаменатель q несократимой дроби 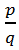  не имеет других простых делителей, кроме 2 и 5, то эту дробь можно записать как конечную десятичную дробь. 

Например, .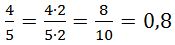 

Если знаменатель q несократимой дроби 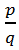  имеет простой делитель, не равный 2 и 5, то эту дробь нельзя записать как конечную десятичную дробь. 

Например, 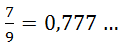. Это бесконечная периодическая дробь. . Число 7 – это период дроби. Это число повторяется в записи дроби бесконечное число раз. 

Читаем периодические дроби так: 

 – «нуль целых и семь в периоде»; 

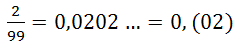 – «нуль целых и нуль два в периоде»; 

 – «три целых, одна десятая и семь в периоде». 

К любому целому числу или конечной десятичной дроби можно справа приписать бесконечно много нулей. Это значит, что любое целое число или конечную десятичную дробь можно записать как бесконечную периодическую дробь с периодом нуль. 

Любое целое число или конечная десятичная дробь – это частный случай бесконечной периодической дроби. 

Чтобы выполнить действия с обыкновенными и десятичными дробями, нужно все числа записать как обыкновенные дроби или все числа записать как конечные десятичные дроби и выполнить действия. 

Например, найдём значение выражения  .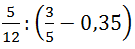 

1. Сначала выполним вычитание:

. 

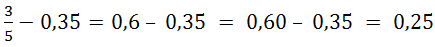2.  Затем выполним деление:

  

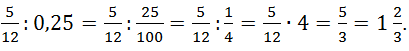
Таким образом, мы нашли точное значение выражения.