Рассмотрим прямую линию (рис. 1). Обозначим её направление вправо знаком   (стрелка). 

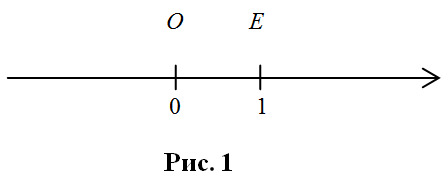
Будем рассматривать это направление как положительное, а противоположное направление (влево) как отрицательное. 

Мы получили ось. Возьмём на ней точку и обозначим её буквой О. Точка О изображает число 0 (нуль). Это начало отсчёта. Возьмём любую точку справа от точки О и обозначим её буквой Е. Будем считать, что отрезок ОЕ – это единица длины (то есть длина отрезка ОЕ равна 1). Точка Е изображает число 1. 

Мы получили числовую (координатную) ось. 

Прямая, на которой выбраны начало отсчёта, положительное направление и единица длины, называется координатной осью. 

На рисунке 1 координатная ось изображена горизонтально с положительным направлением, которое идёт вправо от точки О. 

Начало отсчёта (начальная точка) О делит координатную ось на два луча. Один из них идёт вправо от точки О в положительном направлении. Это положительный луч. Другой луч идёт влево от точки O. Это отрицательный луч. 

Каждая точка координатной оси изображает действительное число. Если точка находится на положительном луче, то она изображает положительное число. Если точка находится на отрицательном луче, то она изображает отрицательное число. 

Число, которое обозначено на координатной оси точкой, называют координатой этой точки. 

Каждой точке координатной оси соответствует действительное число – координата этой точки (рис. 2). 

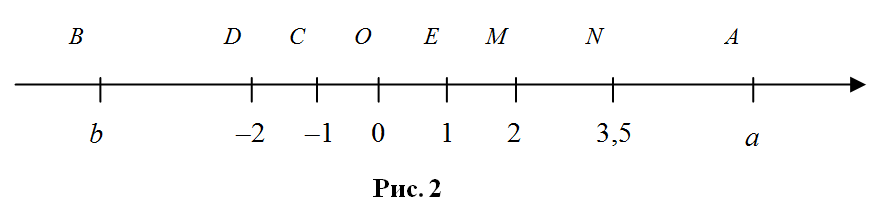
Две различные точки A и B координатной оси имеют разные координаты a и b. Если точка A расположена справа от точки B, то a > b. 

Каждое действительное число есть координата некоторой точки координатной оси. 

Зададим на плоскости две оси координат так, чтобы угол между ними был прямой (90°). Такие прямые называются перпендикулярными. Назовём их ось x и ось y. Точку пересечения обозначим точкой О. Эта точка является началом отсчёта для каждой из этих осей. Единицы длины осей возьмём равными друг другу. 

На плоскости определена прямоугольная (декартова) система координат xOy (рис. 3). 

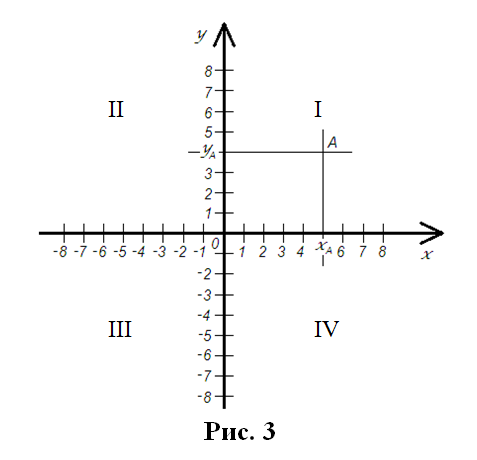
Ось x – это ось абсцисс. Ось y – это ось ординат. Точка О – начало системы координат. 

Плоскость, на которой задана декартова система координат, называется координатной плоскостью. 

Прямоугольная система координат xOy разделяет плоскость на четыре части, которые называются координатными углами. Их обозначают римскими числами I, II, III, IV (рис. 3). 

Пусть A – произвольная точка координатной плоскости. Проведём через точку A прямые, которые параллельны осям координат. Эти прямые пересекают оси координат. Координаты точек пересечения – это координаты точки А. 

x_A – это первая координата (абсцисса) точки А. 

y_A – это вторая координата (ордината) точки А. 

Говорят, что точка А имеет координаты x_A, y_A, и пишут А(x_A, y_A). 

Например, на рисунке 3 изображена точка А, которая имеет абсциссу x = 5 и ординату y = 4, поэтому пишут А(5; 4). 

Пару координат (x_A, y_A) точки А называют упорядоченной парой. Их нельзя менять местами. Если пара состоит из разных чисел, то после их перестановки получится другая точка плоскости. 

Итак, если на плоскости задана прямоугольная система координат xOy, то:

1) каждой точке плоскости поставлена в соответствие упорядоченная пара чисел (пара координат точки);

2) разным точкам плоскости поставлены в соответствие разные упорядоченные пары чисел;

3) каждая упорядоченная пара чисел соответствует некоторой точке плоскости.